Курс лекций по теоретической механике. Динамика
государственное автономное учреждение
Калининградской области
профессиональная образовательная организация
Колледж сервиса и туризма
Курс лекций с примерами практических заданий
«Основы теоретической механики»
по дисциплине Техническая механика
для студентов 3 курса
специальности 20.02.04 Пожарная безопасность
Калининград
УТВЕРЖДАЮ
Заместитель директора по УР ГАУ КО ПОО КСТН.Н. Мясникова
ОДОБРЕНО
Методическим советом ГАУ КО ПОО КСТ
РАССМОТРЕНО
На заседании ПЦК
Редакционная коллегия:
Колганова А.А., методист
Фалалеева А.Б., преподаватель русского языка и литературы
Цветаева Л.В.., председатель ПЦК общематематических и естественнонаучных дисциплин
Составитель:
Незванова И.В. преподаватель ГАУ КО ПОО КСТ
Содержание
Теоретические сведения
Теоретические сведения
Примеры решения практических задач
Динамика: основные понятия и аксиомы
Теоретические сведения
Примеры решения практических задач
Список литературы
Теоретические сведения
Статика: основные понятия и аксиомы.
Статика – раздел теоретической механики, в котором рассматривают свойства сил, приложенных к точкам твердого тела, и условия их равновесия. Основные задачи:
1. Преобразования систем сил в эквивалентные системы сил.
2. Определение условий равновесия систем сил, действующих на твердое тело.
Материальной точкой называют простейшую модель материального тела
любой формы, размеры которого достаточно малы и которое можно принять за геометрическую точку, имеющую определенную массу. Механической системой называется любая совокупность материальных точек. Абсолютно твёрдым телом называют механическую систему, расстояния, между точками которой не изменяются при любых взаимодействиях.
Сила – это мера механического взаимодействия материальных тел между собой. Сила – величина векторная, так как она определяется тремя элементами:
численным значением;
направлением;
точкой приложения (А).
Единица измерения силы – Ньютон(Н).

Рисунок 1.1
Система сил – это совокупность сил, действующих на какое – либо тело.
Уравновешенной (равной нулю) системой сил называется, такая система, которая будучи, приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Аксиомы статики.
Аксиома 1: Если к телу приложена уравновешенная система сил, то оно движется равномерно и прямолинейно или находится в состоянии покоя (закон инерции).
Аксиома 2:
Абсолютно твердое тело находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Рисунок 1.2

Аксиома 3:
Механическое состояние тела не нарушится, если к действующей на него системе сил добавить или от неё отнять уравновешенную систему сил.

Аксиома 4: Равнодействующая двух приложенных к телу сил равна их геометрической сумме, то есть выражается по модулю и направлению диагональю параллелограмма, построенного на этих силах как на сторонах.
Рисунок 1.3.
Аксиома 5:
Силы, с которыми действуют друг на друга два тела, всегда равны по модулю и направлены вдоль одной прямой в противоположные стороны.

Рисунок 1.4.
Виды связей и их реакции
Связями
называются любые ограничения, препятствующие перемещению тела в пространстве. Тело, стремясь под действием приложенных сил осуществить перемещение, которому препятствует связь, будет действовать на нее с некоторой силой, называемой
силой давления на связь
. По закону о равенстве действия и противодействия, связь будет действовать на тело с такой же по модулю, но противоположно направленной силой.
Сила, с которой данная связь действует на тело, препятствуя тем или иным перемещениям, называется
силой реакции (реакцией) связи
.
Одним из основных положений механики является
принцип освобождаемости от связей
:
всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями связей.
Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу. Основные виды связей и их реакции приведены в таблице 1.1.
Таблица 1.1
Виды связей и их реакции
Наименование связи
1
Гладкая поверхность (опора)
– поверхность (опора), трением о которую данного тела можно пренебречь.
При свободном опирании реакция
направляется перпендикулярно касательной, проведенной через точку
А
контакта тела
1
с опорной поверхностью
2
.

2
Нить (гибкая, нерастяжимая). Связь, осуществлённая в виде нерастяжимой нити, не позволяет телу удаляться от точки подвеса. Поэтому реакция нити направлена вдоль нити к точке её подвеса.

3
Невесомый стержень
– стержень, весом которого по сравнению с воспринимаемой нагрузкой можно пренебречь.
Реакция невесомого шарнирно прикрепленного прямолинейного стержня направлена вдоль оси стержня.

4
Подвижный шарнир, шарнирно-подвижная опора. Реакция направлена по нормали к опорной поверхности.

7
Жесткая заделка.
В плоскости жесткой заделки будут две составляющие реакции
,
и момент пары сил
, который препятствует повороту балки
1
относительно точки
А
.
Жесткая заделка в пространстве отнимает у тела 1 все шесть степеней свободы – три перемещения вдоль осей координат и три поворота относительно этих осей.
В пространственной жесткой заделке будут три составляющие
,
,
и три момента пар сил
![]() .
.

Система сходящихся сил
Системой сходящихся сил
называется система сил, линии действия которых пересекаются в одной точке. Две силы, сходящиеся в одной точке, согласно третьей аксиоме статики можно заменить одной силой –
равнодействующей
.
Главный вектор системы сил
– величина, равная геометрической сумме сил системы.
Равнодействующую плоской системы сходящихся сил можно определить графически и аналитически .
Сложение системы сил . Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (рис. 1.5), либо путём построения силового многоугольника (рис. 1.6).


Рисунок 1.5Рисунок 1.6
Проекция силы на ось
– алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси.
Проекция
F
x
(рис.1.7) силы
на ось
х
положительна, если угол α острый, отрицательна - если угол α тупой. Если сила
перпендикулярна оси, то ее проекция на ось равна нулю.

Рисунок 1.7
Проекция силы на плоскость Оху – вектор , заключенный между проекциями начала и конца силы на эту плоскость. Т.е. проекция силы на плоскость величина векторная, характеризуется не только числовым значением, но и направлением в плоскости Оху (рис.1.8).

Рисунок 1.8
Тогда модуль проекции на плоскость Оху будет равен:
F xy = F cosα,
где α - угол между направлением силы
и ее проекцией
.
Аналитический способ задания сил
.
Для аналитического способа задания силы
необходимо выбрать систему координатных осей
Охуz
, по отношению к которой будет определяться направление силы в пространстве.
Вектор, изображающий силу
, можно построить, если известны модуль этой силы и углы α, β, γ, которые сила образует с координатными осями. Точка
А
приложения силы
задается отдельно своими координатами
х
,
у
,
z
. Можно задавать силу ее проекциями
Fx
,
Fy
,
Fz
на координатные оси. Модуль силы в этом случае определится по формуле:
![]()
а направляющие косинусы:
,
.
Аналитический способ сложения сил : проекция вектора суммы на какую нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось, т.е., если:
то
,
,
.
Зная
Rx, Ry, Rz
, можем определить модуль
![]()
и направляющие косинусы:
, , .
Рисунок 1.9
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю.1) Геометрическое условие равновесия сходящейся системы сил : для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил,
был замкнут (конец вектора последней слагаемой
силы должен совместиться с началом вектора первой слагаемой силы). Тогда главный вектор системы сил будет равен нулю ()
2)
Аналитические условия равновесия
.
Модуль главного вектора системы сил определяется по формуле
.
![]() =0. Поскольку
, то подкоренное выражение может быть равно нулю только в том случае, если каждое слагаемое одновременно обращается в нуль, т.е.
=0. Поскольку
, то подкоренное выражение может быть равно нулю только в том случае, если каждое слагаемое одновременно обращается в нуль, т.е.
Rx = 0, Ry = 0, R z = 0.
Следовательно, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трёх координат осей были равны нулю:
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил на каждую из двух координатных осей были равны нулю:
Сложение двух параллельных сил, направленных в одну сторону.

Рисунок 1.9
Две параллельные силы, направленные в одну сторону, приводятся к одной равнодействующей силе, им параллельной и направленной в ту же сторону. Величина равнодействующей равна сумме величин данных сил, а точка ее приложения С делит расстояние между линиями действия сил внутренним образом на части, обратно пропорциональные величинам этих сил, то естьB A C
R=F 1 +F 2
Сложение двух не равных по величине параллельных сил, направленных в противоположные стороны.
Две не равные по величине антипараллельные силы приводятся к одной равнодействующей силе им параллельной и направленной в сторону большей силы. Величина равнодействующей равна разности величин данных сил, а точка ее приложения С, делит расстояние между линиями действия сил внешним образом на части, обратно пропорциональные величинам этих сил, то есть
Пара сил и момент силы относительно точки.
Моментом силы
относительно точки О называется, взятое с соответствующим знаком, произведение величины силы на расстояние h от точки О до линии действия силы
. Это произведение берётся со знаком плюс, если сила
стремится вращать тело против хода часовой стрелки, и со знаком -, если сила
стремится вращать тело по ходу часовой стрелки, то есть
. Длина перпендикуляра h называется
плечом силы
точки О. Эффект действия силы т.е. угловое ускорение тела больше, чем больше величина момента силы.

Рисунок 1.11
Парой сил называется система, состоящая из двух равных по величине параллельных сил, направленных в противоположные стороны. Расстояние h между линиями действия сил называется плечом пары . Моментом пары сил m(F,F") называется взятое с соответствующим знаком произведение величины одной из сил, составляющих пару на плечо пары.Записывается это так: m(F, F")= ± F × h , где произведение берется со знаком плюс, если пара сил стремится вращать тело против хода часовой стрелки и со знаком минус, если пара сил стремится вращать тело по ходу часовой стрелки.
Теорема о сумме моментов сил пары.
Сумма моментов сил пары (F,F") относительно любой точки 0, взятой в плоскости действия пары, не зависит от выбора этой точки и равна моменту пары.
Теорема об эквивалентных парах. Следствия.
Теорема. Две пары, моменты которых равны между собой, эквивалентны, т.е. (F, F") ~ (P,P")
Следствие 1 . Пару сил можно переносить в любое место плоскости ее действия, а также поворачивать на любой угол и изменять плечо и величину сил пары, сохраняя при этом момент пары.
Следствие 2. Пара сил не имеет равнодействующей и не может быть уравновешена одной силой, лежащей в плоскости пары.

Рисунок 1.12
Сложение и условие равновесия системы пар на плоскости.
1. Теорема о сложении пар, лежащих в одной плоскости. Систему пар, как угодно расположенных в одной плоскости, можно заменить одной парой, момент которой равен сумме моментов данных пар.
2. Теорема о равновесии системы пар на плоскости.
Для того, чтобы абсолютно твердое тело находилось в состоянии покоя под действием системы пар, как угодно расположенных в одной плоскости, необходимо и достаточно, чтобы сумма моментов всех пар была равна нулю, то есть
Центр тяжести
Сила тяжести – равнодействующая сил притяжения к Земле, распределённых по всему объему тела.
Центр тяжести тела – это такая неизменно связанная с этим телом точка, через которую проходит линия действия силы тяжести данного тела при любом положении тела в пространстве.
Методы нахождения центра тяжести
1. Метод симметрии:
1.1. Если однородное тело имеет плоскость симметрии, то центр тяжести лежит в этой плоскости
1.2. Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси. Центр тяжести однородного тела вращения лежит на оси вращения.
1.3 Если однородное тело имеет две оси симметрии, то центр тяжести находится в точке их пересечения.
2. Метод разбиения: Тело разбивается на наименьшее число частей, силы тяжести и положение центров тяжести которых известны.
3. Метод отрицательных масс: При определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но массу свободных полостей считать отрицательной.
Координаты центра тяжести плоской фигуры:

Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам. (рисунок 1.13)

Примечание: Центр тяжести симметрии фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты.
1.2. Примеры решения практических задач
Пример 1:
Груз подвешен на стержне и находится в равновесии. Определить усилия в стержне. (рисунок 1.2.1)

Решение:
Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз. (5-я аксиома)
Определяем возможные направления реакций связей «жесткие стержни».
Усилия направлены вдоль стержней.
Рисунок 1.2.1.
Освободим точку А от связей, заменив действие связей их реакциями. (рисунок 1.2.2)
Построение начнём с известной силы, вычертив вектор F в некотором масштабе.
Из конца вектора F проводим линии, параллельные реакциям R 1 и R 2 .
Рисунок 1.2.2
Пересекаясь, линии создают треугольник. (рисунок 1.2.3.). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.
Для более точных расчётов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла – величина постоянная
![]()
Для данного случая:
Рисунок 1.2.3
![]()
Замечание: Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
Пример 2:
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом.

Решение:
Рисунок 1.2.4
1. Определяем проекции всех сил системы на Ох (рисунок 1.2.4)Сложив алгебраически проекции, получим проекцию равнодействующей на ось Ох.

Знак говорит о том, что равнодействующая направлена влево.
2. Определяем проекции всех сил на ось Оу:
Сложив алгебраически проекции, получим проекцию равнодействующей на ось Оу.
Знак говорит о том, что равнодействующая направлена вниз.
3. Определяем модуль равнодействующей по величинам проекций:
4. Определим значение угла равнодействующей с осью Ох:

и значение угла с осью Оу:
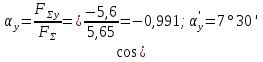
Пример 3:
Расчитать сумму моментов сил относительно точки О (рисунок 1.2.6).

ОА = АВ = В D=DE=CB=2 м
Рисунок 1.2.6
Решение:
1. Момент силы относительно точки численно равен произведению модуля на плечо силы.
2. Момент силы равен нулю, если линия действия силы проходит через точку.
Пример 4:
Определить положение центра тяжести фигуры, представленной на рисунке 1.2.7

Решение:
Разбиваем фигуру на три:
1-прямоугольник
А 1 =10*20=200см 2
2-треугольник
А 2 =1/2*10*15=75см 2
3-круг
А 3 =3,14*3 2 =28,3см 2
ЦТ фигуры 1: х 1 =10см, у 1 =5см
ЦТ фигуры 2: х 2 =20+1/3*15=25см, у 2 =1/3*10=3,3см
ЦТ фигуры 3: х 3 =10см, у 3 =5см
Аналогично определяется у с =4,5см
Кинематика: основные понятия.
Основные кинематические параметры
Траектория - линия, которую очерчивает материальная точка при движении в пространстве. Траектория может быть прямой и кривой, плоской и пространственной линией.
Уравнение траектории при плоском движении: у = f ( x )
Пройденный путь. Путь измеряется вдоль траектории в направлении движения. Обозначение - S , единицы измерения - метры.
Уравнение движения точки –это уравнение, определяющее положение движущейся точки в зависимости от времени.
Рисунок 2.1
Положение точки в каждый момент времени можно определить по расстоянию, пройденному вдоль траектории от некоторой неподвижной точки, рассматриваемой как начало отсчета (рисунок 2.1). Такой способ задания движения называется естественным . Таким образом, уравнение движения можно представить в виде S = f (t).

Рисунок 2.2
Положение точки можно также определить, если известны ее координаты в зависимости от времени (рисунок 2.2). Тогда в случае движения на плоскости должны быть заданы два уравнения:В случае пространственного движения добавляется и третья координата z = f 3 ( t )
Такой способ задания движения называют координатным .
Скорость движения – это векторная величина, характеризующая в данный момент быстроту и направление движения по траектории.
Скорость - вектор, в любой момент направленный по касательной к траектории в сторону направления движения (рисунок 2.3).

Рисунок 2.3
Если точка за равные промежутки времени проходит равные расстояния, то движение называют равномерным .Средняя скорость на пути Δ S определяется:
где ΔS - пройденный путь за время Δ t ; Δ t - промежуток времени.
Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным . В этом случае скорость - величина переменная и зависит от времени v = f ( t )
Скорость в данный момент определяют как
Ускорение точки - векторная величина, характеризующая быстроту изменения скорости по величине и направлению.
Скорость точки при перемещении из точки М1 в точку Мг меняется по величине и направлению. Среднее значение ускорения за этот промежуток времени
Ускорение в данный момент:
Обычно для удобства рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательное (рисунок 2.4)
Нормальное ускорение а n , характеризует изменение скорости по
направлению и определяется как
Нормальное ускорение всегда направлено перпендикулярно скорости к центру дуги.

Рисунок 2.4
Касательное ускорение а t , характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а при замедлении оно направлено противоположно направлению вектора скорости.![]()
Значение полного ускорения определяется, как:
Анализ видов и кинематических параметров движений
Равномерное движение – это движение с постоянной скоростью:
Для прямолинейного равномерного движения:
Для криволинейного равномерного движения:
![]()
Закон равномерного движения :
Равнопеременное движение – это движение с постоянным касательным ускорением:
Для прямолинейного равнопеременного движения
Для криволинейного равнопеременного движения:
![]()
Закон равнопеременного движения:
![]()
Кинематические графики
Кинематические графики – это графики изменения пути, скорости и ускорений в зависимости от времени.
Равномерное движение (рисунок 2.5)

Рисунок 2.5
Равнопеременное движение (рисунок 2.6)

Рисунок 2.6
Простейшие движения твёрдого тела
Поступательным движением называют движение твёрдого тела, при котором всякая прямая линия на теле при движении остаётся параллельной своему начальному положению (рисунок 2.7)

Рисунок 2.7
При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы.
При
вращательном движении
все точки тела описывают окружности вокруг общей неподвижной оси.

Неподвижная ось, вокруг которой вращаются все точки тела, называют осью вращения.
Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры. (рисунок 2.8)
φ – угол поворота тела;
ω – угловая скорость, определяет изменение угла поворота в единицу времени;
Изменение угловой скорости во времени определяется угловым ускорением:
2.2. Примеры решения практических задач
Пример 1: Дано уравнение движения точки. Определить скорость точки в конце третьей секунды движения и среднюю скорость за первые три секунды.
![]()
Решение:
1. Уравнение скорости
2. Скорость в конце третьей секунды (t =3 c )
3. Средняя скорость
Пример 2: По заданному закону движения определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
![]()
Решение:
1. Вид движения: равнопеременное (![]() )
)
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчёта 10м;
- начальная скорость 20м/с
- постоянное касательное ускорение
![]()
- ускорение отрицательное, следовательно, движение замедленное, ускорение направлено в сторону противоположную скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю.
3.Динамика: основные понятия и аксиомы
Динамика – раздел теоретической механики, в котором устанавливается связь между движение тел и действующими на них силами.
В динамике решают два типа задач:
определяют параметры движения по заданным силам;
определяют силы, действующие на тело, по заданным кинематическим параметрам движения.
Под
материальной точкой
подразумевают некое тело, имеющее определенную массу (т. е. содержащее некоторое количество материи), но не имеющее линейных размеров (бесконечно малый объем пространства).
Изолированной
считается материальная точка, на которую не оказывают действие другие материальные точки. В реальном мире изолированных материальных точек, как и изолированных тел, не существует, это понятие является условным.
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку.
Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела.
При вращательном движении тела точки могут двигаться не одинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
Аксиомы динамики
Первая аксиома ( принцип инерции): в сякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Это состояние называют состоянием инерции. Вывести точку из этого состояния, т.е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы - килограмм (кг).
Вторая аксиома (второй закон Ньютона - основной закон динамики)
F=ma
где т - масса точки, кг; а - ускорение точки, м/с 2 .
Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли:
G = mg,
где g - 9,81 м/с² , ускорение свободного падения.
Третья аксиома (третий закон Ньютона): с илы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны .
При взаимодействии ускорения обратно пропорциональны массам.
Четвертая аксиома (закон независимости действия сил): к аждая сила системы сил действует так, как она действовала бы одна.
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности (рисунок 3.1):

Рисунок 3.1
Понятие о трении. Виды трения.
Трение-
сопротивление возникающее при движении одного шероховатого тела по поверхности другого. При скольжении тел возникает трение скольжения, при качении – трение качания.

Трение скольжения
Рисунок 3.2.
Причина – механическое зацепление выступов. Сила сопротивления движению при скольжении называется силой трения скольжения (рисунок 3.2)Законы трения скольжения:
1. Сила трения скольжения прямо пропорциональна силе нормального давления:

где R -сила нормального давления, направлена перпендикулярно опорной поверхности; f - коэффициент трения скольжения.
Рисунок 3.3.
В случае движения тела по наклонной плоскости (рисунок 3.3)Трение качения
Сопротивление при качении связано с взаимной деформацией грунта и колеса и значительно меньше трения скольжения.

Для равномерного качения колеса необходимо прикладывать силу F дв (рисунок 3.4)
Условие качения колеса состоит в том, что движущийся момент должен быть не меньше момента сопротивления:
Рисунок 3.4.
Пример 1: Пример 2: К двум материальным точкам массой m 1 =2кг и m 2 = 5 кг приложены одинаковые силы. Сравните величины ускоренней.Решение:
Согласно третей аксиоме динамики ускорения обратно пропорциональны массам:
![]()
Пример 3:
Определите работу силы тяжести при перемещении груза из точки А в точку С по наклонной плоскости (рисунок 3. 7). Сила тяжести тела 1500Н. АВ= 6 м, ВС=4м.
Пример 3:
Определите работу силы резания за 3 мин. Скорость вращения детали 120 об/мин, диаметр обрабатываемой детали 40мм, сила резания 1кН. (рисунок 3.8)

Решение:
1. Работа при вращательном движении:
2. Угловая частота вращения 120 об/мин
Рисунок 3.8 .
3. Число оборотов за заданное время составляет z =120*3=360 об.Угол поворота за это время φ=2π z =2*3,14*360=2261рад
4. Работа за 3 оборота: W =1*0,02*2261=45,2 кДж
Список литературы
Олофинская, В.П. « Техническая механика», Москва «Форум»2011г.
Эрдеди А.А. Эрдеди Н.А. Теоретическая механика. Сопротивление материалов.- Р-н-Д; Феникс, 2010
Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.
Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.
Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.
Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.
Статика твердого тела
Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.
- Основные понятия и законы статики
- Абсолютно твердое тело (твердое тело, тело) – это материальное тело, расстояние между любыми точками в котором не изменяется.
- Материальная точка – это тело, размерами которого по условиям задачи можно пренебречь.
- Свободное тело – это тело, на перемещение которого не наложено никаких ограничений.
- Несвободное (связанное) тело – это тело, на перемещение которого наложены ограничения.
- Связи – это тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).
- Реакция связи — это сила, характеризующая действие связи на твердое тело. Если считать силу, с которой твердое тело действует на связь, действием, то реакция связи является противодействием. При этом сила - действие приложена к связи, а реакция связи приложена к твердому телу.
- Механическая система – это совокупность взаимосвязанных между собой тел или материальных точек.
- Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.
- Сила
– это векторная величина, характеризующая механическое действие одного материального тела на другое.
Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон. - Линия действия силы – это прямая, вдоль которой направлен вектор силы.
- Сосредоточенная сила – сила, приложенная в одной точке.
- Распределенные силы (распределенная нагрузка)
– это силы, действующие на все точки объема, поверхности или длины тела.
Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).
Размерность распределенной нагрузки – Н/м 3 (Н/м 2 , Н/м). - Внешняя сила – это сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.
- Внутренняя сила – это сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.
- Система сил – это совокупность сил, действующих на механическую систему.
- Плоская система сил – это система сил, линии действия которых лежат в одной плоскости.
- Пространственная система сил – это система сил, линии действия которых не лежат в одной плоскости.
- Система сходящихся сил – это система сил, линии действия которых пересекаются в одной точке.
- Произвольная система сил – это система сил, линии действия которых не пересекаются в одной точке.
- Эквивалентные системы сил
– это такие системы сил, замена которых одна на другую не изменяет механического состояния тела.
Принятое обозначение: . - Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.
- Уравновешенная система сил
– это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).
 .
. - Равнодействующая сила
– это сила, действие которой на тело эквивалентно действию системы сил.
 .
. - Момент силы – это величина, характеризующая вращающую способность силы.
- Пара сил
– это система двух параллельных равных по модулю противоположно направленных сил.
Принятое обозначение: .
Под действием пары сил тело будет совершать вращательное движение. - Проекция силы на ось
– это отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси.
Проекция положительна, если направление отрезка совпадает с положительным направлением оси. - Проекция силы на плоскость – это вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости.
- Закон 1 (закон инерции).
Изолированная материальная точка находится в покое либо движется равномерно и прямолинейно.
Равномерное и прямолинейное движение материальной точки является движением по инерции. Под состоянием равновесия материальной точки и твердого тела понимают не только состояние покоя, но и движение по инерции. Для твердого тела существуют различные виды движения по инерции, например равномерное вращение твердого тела вокруг неподвижной оси. - Закон 2.
Твердое тело находится в равновесии под действием двух сил только в том случае, если эти силы равны по модулю и направлены в противоположные стороны по общей линии действия.
Эти две силы называются уравновешивающимися.
Вообще силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в покое. - Закон 3.
Не нарушая состояния (слово «состояние» здесь означает состояние движения или покоя) твердого тела, можно добавлять и отбрасывать уравновешивающиеся силы.
Следствие. Не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела.
Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела. - Закон 4.
Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой
диагонали.
По модулю равнодействующая равна: - Закон 5 (закон равенства действия и противодействия)
. Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны по одной прямой.
Следует иметь в виду, что действие - сила, приложенная к телу Б , и противодействие - сила, приложенная к телу А , не уравновешиваются, так как они приложены к разным телам. - Закон 6 (закон отвердевания)
. Равновесие нетвердого тела не нарушается при его затвердевании.
Не следует при этом забывать, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но недостаточными для соответствующего нетвердого тела. - Закон 7 (закон освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив действие связей соответствующими реакциями связей.
- Связи и их реакции
- Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
- Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
- Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
- Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
- Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.




Кинематика
Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.
- Основные понятия кинематики
- Закон движения точки (тела) – это зависимость положения точки (тела) в пространстве от времени.
- Траектория точки – это геометрическое место положений точки в пространстве при ее движении.
- Скорость точки (тела) – это характеристика изменения во времени положения точки (тела) в пространстве.
- Ускорение точки (тела) – это характеристика изменения во времени скорости точки (тела).
- Определение кинематических характеристик точки
- Траектория точки
В векторной системе отсчета траектория описывается выражением: .
В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y) — в пространстве, или y = f(x) – в плоскости.
В естественной системе отсчета траектория задается заранее. - Определение скорости точки в векторной системе координат
При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: .
Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): .
.
Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
Вывод: скорость точки – векторная величина, равная производной от закона движения по времени.
Свойство производной: производная от какой либо величины по времени определяет скорость изменения этой величины. - Определение скорости точки в координатной системе отсчета
Скорости изменения координат точки: .
.
Модуль полной скорости точки при прямоугольной системе координат будет равен: .
.
Направление вектора скорости определяется косинусами направляющих углов: ,
,
где — углы между вектором скорости и осями координат. - Определение скорости точки в естественной системе отсчета
Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: .
Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .
- Кинематика твердого тела
- В кинематике твердых тел решаются две основные задачи:
1) задание движения и определение кинематических характеристик тела в целом;
2) определение кинематических характеристик точек тела. - Поступательное движение твердого тела
Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
Теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения .
Вывод: поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки . - Вращательное движение твердого тела вокруг неподвижной оси
Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
Закон вращательного движения тела вокруг неподвижной оси .
Угловую скорость и угловое ускорение тела определим методом дифференцирования:
— угловая скорость, рад/с;
— угловое ускорение, рад/с².
Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М , то точка М будет описывать вокруг точки С окружность радиуса R . За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .
.
Модуль линейной скорости: .
.
Ускорение точки М при известной траектории определяется по его составляющим : ,
,
где .
.
В итоге, получаем формулы
тангенциальное ускорение: ;
;
нормальное ускорение: .
.

Динамика
Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.
- Основные понятия динамики
- Инерционность — это свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.
- Масса — это количественная мера инерционности тела. Единица измерения массы — килограмм (кг).
- Материальная точка — это тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.
- Центр масс механической системы
— геометрическая точка, координаты которой определяются формулами:
где m k , x k , y k , z k — масса и координаты k -той точки механической системы, m — масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести. - Момент инерции материального тела относительно оси
– это количественная мера инертности при вращательном движении.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси: .
.
Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:
- Сила инерции материальной точки — это векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения:
- Сила инерции материального тела
— это векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс: ,
где — ускорение центра масс тела. - Элементарный импульс силы
— это векторная величина , равная произведению вектора силы на бесконечно малый промежуток времени dt
:
.
Полный импульс силы за Δt равен интегралу от элементарных импульсов: .
. - Элементарная работа силы — это скалярная величина dA , равная скалярному прои
1 слайд
Курс лекций по теоретической механике Динамика (I часть) Бондаренко А.Н. Москва - 2007 Электронный учебный курс написан на основе лекций, читавшихся автором для студентов, обучавшихся по специальностям СЖД, ПГС и СДМ в НИИЖТе и МИИТе (1974-2006 гг.). Учебный материал соответствует календарным планам в объеме трех семестров. Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра Power Point не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional. Замечания и предложения можно послать по e-mail: [email protected] . Московский государственный университет путей сообщения (МИИТ) Кафедра теоретической механики Научно-технический центр транспортных технологий

2 слайд
Содержание Лекция 1. Введение в динамику. Законы и аксиомы динамики материальной точки. Основное уравнение динамики. Дифференциальные и естественные уравнения движения. Две основные задачи динамики. Примеры решения прямой задачи динамики Лекция 2. Решение обратной задачи динамики. Общие указания к решению обратной задачи динамики. Примеры решения обратной задачи динамики. Движение тела, брошенного под углом к горизонту, без учета сопротивления воздуха. Лекция 3. Прямолинейные колебания материальной точки. Условие возникновения колебаний. Классификация колебаний. Свободные колебания без учета сил сопротивления. Затухающие колебания. Декремент колебаний. Лекция 4. Вынужденные колебания материальной точки. Резонанс. Влияние сопротивления движению при вынужденных колебаниях. Лекция 5. Относительное движение материальной точки. Силы инерции. Частные случаи движения для различных видов переносного движения. Влияние вращения Земли на равновесие и движение тел. Лекция 6. Динамика механической системы. Механическая система. Внешние и внутренние силы. Центр масс системы. Теорема о движении центра масс. Законы сохранения. Пример решения задачи на использование теоремы о движении центра масс. Лекция 7. Импульс силы. Количество движения. Теорема об изменении количества движения. Законы сохранения. Теорема Эйлера. Пример решения задачи на использование теоремы об изменении количества движения. Момент количества движения. Теорема об изменении момента количества движения.. Лекция 8. Законы сохранения. Элементы теории моментов инерции. Кинетический момент твердого тела. Дифференциальное уравнение вращения твердого тела. Пример решения задачи на использование теоремы об изменении момента количества движения системы. Элементарная теория гироскопа. Рекомендуемая литература 1. Яблонский А.А. Курс теоретической механики. Ч.2. М.: Высшая школа. 1977 г. 368 с. 2. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука. 1986 г. 416 с. 3. Сборник заданий для курсовых работ /Под ред. А.А. Яблонского. М.:Высшая школа. 1985 г. 366 с. 4. Бондаренко А.Н. “Теоретическая механика в примерах и задачах. Динамика” (электронное пособие www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004 г.

3 слайд
Лекция 1 Динамика – раздел теоретической механики, изучающий механическое движение с самой общей точки зрения. Движение рассматривается в связи с действующими на объект силами. Раздел состоит из трех отделов: Динамика материальной точки Динамика Динамика механической системы Аналитическая механика ■ Динамика точки – изучает движение материальной точки с учетом сил, вызывающих это движение. Основной объект - материальная точка – материальное тело, обладающей массой, размерами которого можно пренебречь. Основные допущения: – существует абсолютное пространство (обладает чисто геометрическими свойствами, не зависящими от материи и ее движения. – существует абсолютное время (не зависит от материи и ее движения). Отсюда вытекает: – существует абсолютно неподвижная система отсчета. – время не зависит от движения системы отсчета. – массы движущихся точек не зависят от движения системы отсчета. Эти допущения используются в классической механике, созданной Галилеем и Ньютоном. Она имеет до сих пор достаточно широкую область применения, поскольку рассматриваемые в прикладных науках механические системы не обладают такими большими массами и скоростями движения, для которых необходим учет их влияния на геометрию пространства, время, движение, как это делается в релятивистской механике (теории относительности). ■ Основные законы динамики – впервые открытые Галилеем и сформулированные Ньютоном составляют основу всех методов описания и анализа движения механических систем и их динамического взаимодействия под действием различных сил. ■ Закон инерции (закон Галилея-Ньютона) – Изолированная материальная точка тело сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, приложенные силы не заставят ее изменить это состояние. Отсюда следует эквивалентность состояния покоя и движения по инерции (закон относительности Галилея). Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной. Свойство материальной точки стремиться сохранить неизменной скорость своего движения (свое кинематическое состояние) называется инертностью. ■ Закон пропорциональности силы и ускорения (Основное уравнение динамики - II закон Ньютона) – Ускорение, сообщаемое материальной точке силой, прямо пропорционально силе и обратно пропорционально массе этой точки: или Здесь m – масса точки (мера инертности), измеряется в кг, численно равна весу, деленному на ускорение свободного падения: F – действующая сила, измеряется в Н (1 Н сообщает точке массой 1 кг ускорение 1 м/c2, 1 Н = 1/9.81 кг-с). ■ Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами взаимодействия, с учетом сил, вызывающих это движение. ■ Аналитическая механика – изучает движение несвободных механических систем с использованием общих аналитических методов. 1

4 слайд
Лекция 1 (продолжение – 1.2) Дифференциальные уравнения движения материальной точки: - дифференциальное уравнение движения точки в векторном виде. - дифференциальные уравнения движения точки в координатном виде. Этот результат может быть получен формальным проецированием векторного дифференциального уравнения (1). После группировки векторное соотношение распадается на три скалярных уравнения: В координатном виде: Используем связь радиуса-вектора с координатами и вектора силы с проекциями: или: Подставим ускорение точки при векторном задании движения в основное уравнение динамики: Естественные уравнения движения материальной точки – получаются проецированием векторного дифференциального уравнения движения на естественные (подвижные) оси координат: или: - естественные уравнения движения точки. ■ Основное уравнение динамики: - соответствует векторному способу задания движения точки. ■ Закон независимости действия сил – Ускорение материальной точки под действием нескольких сил равно геометрической сумме ускорений точки от действия каждой из сил в отдельности: или Закон справедлив для любого кинематического состояния тел. Силы взаимодействия, будучи приложенные к разным точкам (телам) не уравновешиваются. ■ Закон равенства действия и противодействия (III закон Ньютона) – Всякому действию соответствует равное по величине и противоположно направленное противодействие: 2

5 слайд
Две основные задачи динамики: 1. Прямая задача: Задано движение (уравнения движения, траектория). Требуется определить силы, под действием которых происходит заданное движение. 2. Обратная задача: Заданы силы, под действием которых происходит движение. Требуется найти параметры движения (уравнения движения, траекторию движения). Обе задачи решаются с помощью основного уравнения динамики и проекции его на координатные оси. Если рассматривается движение несвободной точки, то как и в статике, используется принцип освобождаемости от связей. В результате реакции связей включаются в состав сил, действующих на материальную точку. Решение первой задачи связано с операциями дифференцирования. Решение обратной задачи требует интегрирования соответствующих дифференциальных уравнений и это значительно сложнее, чем дифференцирование. Обратная задача сложнее прямой задачи. Решение прямой задачи динамики - рассмотрим на примерах: Пример 1. Кабина весом G лифта поднимается тросом с ускорением a . Определить натяжение троса. 1. Выбираем объект (кабина лифта движется поступательно и ее можно рассматривать как материальную точку). 2. Отбрасываем связь (трос) и заменяем реакцией R. 3. Составляем основное уравнение динамики: Определяем реакцию троса: Определяем натяжение троса: При равномерном движении кабины ay = 0 и натяжение троса равно весу: T = G. При обрыве троса T = 0 и ускорение кабины равно ускорению свободного падения: ay = -g. 3 4. Проецируем основное уравнение динамики на ось y: y Пример 2. Точка массой m движется по горизонтальной поверхности (плоскости Oxy) согласно уравнениям: x = a coskt, y = b coskt. Определить силу, действующую на точку. 1. Выбираем объект (материальную точку). 2. Отбрасываем связь (плоскость) и заменяем реакцией N. 3. Добавляем к системе сил неизвестную силу F. 4. Составляем основное уравнение динамики: 5. Проецируем основное уравнение динамики на оси x,y: Определяем проекции силы: Модуль силы: Направляющие косинусы: Таким образом, величина силы пропорциональна расстоянию точки до центра координат и направлена к центру по линии, соединяющей точку с центром. Траектория движения точки представляет собой эллипс с центром в начале координат: O r Лекция 1 (продолжение – 1.3)

6 слайд
Лекция 1 (продолжение 1.4) Пример 3: Груз весом G подвешен на тросе длиной l и движется по круговой траектории в горизонтальной плоскости с некоторой скоростью. Угол отклонения троса от вертикали равен. Определить натяжение троса и скорость груза. 1. Выбираем объект (груз). 2. Отбрасываем связь (трос) и заменяем реакцией R. 3. Составляем основное уравнение динамики: Из третьего уравнения определяем реакцию троса: Определяем натяжение троса: Подставляем значение реакции троса, нормального ускорения во второе уравнение и определяем скорость груза: 4. Проецируем основное уравнение динамики на оси,n, b: Пример 4: Автомашина весом G движется по выпуклому мосту (радиус кривизны равен R) со скоростью V. Определить давление автомашины на мост. 1. Выбираем объект (автомашина, размерами пренебрегаем и рассматриваем как точку). 2. Отбрасываем связь (шероховатую поверхность) и заменяем реакциями N и силой трения Fтр. 3. Составляем основное уравнение динамики: 4. Проецируем основное уравнение динамики на ось n: Отсюда определяем нормальную реакцию: Определяем давление автомашины на мост: Отсюда можно определить скорость, соответствующую нулевому давлению на мост (Q = 0): 4

7 слайд
Лекция 2 После подстановки найденных значений постоянных получаем: Таким образом, под действием одной и той же системы сил материальная точка может совершать целый класс движений, определяемых начальными условиями. Начальные координаты учитывают исходное положение точки. Начальная скорость, задаваемая проекциями, учитывает влияние на ее движение по рассматриваемому участку траектории сил, действовавших на точку до прихода на этот участок, т.е. начальное кинематическое состояние. Решение обратной задачи динамики – В общем случае движения точки силы, действующие на точку, являются переменными, зависящими от времени, координат и скорости. Движение точки описывается системой трех дифференциальных уравнений второго порядка: После интегрирования каждого из них будет шесть постоянных C1, C2,…., C6: Значения постоянных C1, C2,…., C6 находятся из шести начальных условий при t = 0: Пример 1 решения обратной задачи: Свободная материальная точка массы m движется по действием силы F, постоянной по модулю и величине. . В начальный момент скорость точки составляла v0 и совпадала по направлению с силой. Определить уравнение движение точки. 1. Составляем основное уравнение динамики: 3. Понижаем порядок производной: 2. Выберем декартову систему отсчета, направляя ось x вдоль направления силы и спроецируем основное уравнение динамики на эту ось: или x y z 4. Разделяем переменные: 5. Вычисляем интегралы от обоих частей уравнения: 6. Представим проекцию скорости как производную координаты по времени: 8. Вычисляем интегралы от обоих частей уравнения: 7. Разделяем переменные: 9. Для определения значений постоянных C1 и C2 используем начальные условия t = 0, vx = v0 , x = x0: В итоге получаем уравнение равнопеременного движения (по оси x): 5

8 слайд
Общие указания к решению прямой и обратной задачи. Порядок решения: 1. Составление дифференциального уравнения движения: 1.1. Выбрать систему координат – прямоугольную (неподвижную) при неизвестной траектории движения, естественную (подвижную) при известной траектории, например, окружность или прямая линия. В последнем случае можно использовать одну прямолинейную координату. Начало отсчета совместить с начальным положением точки (при t = 0) или с равновесным положением точки, если оно существует, например, при колебаниях точки. 6 1.2. Изобразить точку в положении, соответствующем произвольному моменту времени (при t > 0) так, чтобы координаты были положительными (s > 0, x > 0). При этом считаем также, что проекция скорости в этом положении также положительна. В случае колебаний проекция скорости меняет знак, например, при возвращении к положению равновесия. Здесь следует принять, что в рассматриваемый момент времени точка удаляется от положения равновесия. Выполнение этой рекомендации важно в дальнейшем при работе с силами сопротивления, зависящими от скорости. 1.3. Освободить материальную точку от связей, заменить их действие реакциями, добавить активные силы. 1.4. Записать основной закон динамики в векторном виде, спроецировать на выбранные оси, выразить задаваемые или реактивные силы через переменные время, координаты или скорости, если они от них зависят. 2. Решение дифференциальных уравнений: 2.1. Понизить производную, если уравнение не приводится к каноническому (стандартному) виду. например: или 2.2. Разделить переменные, например: или 2.4. Вычислить неопределенные интегралы в левой и правой частях уравнения, например: 2.3. Если в уравнении три переменных, то сделать замену переменных, например: и затем разделить переменные. Замечание. Вместо вычисления неопределенных интегралов можно вычислить определенные интегралы с переменным верхним пределом. Нижние пределы представляют начальные значения переменных (начальные условия) .Тогда не требуется отдельного нахождения постоянной, которая автоматически включается в решение, например: Используя начальные условия, например, t = 0, vx = vx0, определить постоянную интегрирования: 2.5. Выразить скорость через производную координаты по времени, например, и повторить пункты 2.2 -2.4 Замечание. Если уравнение приводится к каноническому виду, имеющему стандартное решение, то это готовое решение и используется. Постоянные интегрирования по прежнему находятся из начальных условий. См., например, колебания (лекция 4, стр.8). Лекция 2 (продолжение 2.2)

9 слайд
Лекция 2 (продолжение 2.3) Пример 2 решения обратной задачи: Сила зависит от времени. Груз весом P начинает двигаться по гладкой горизонтальной поверхности под действием силы F, величина которой пропорциональна времени (F = kt). Определить пройденное расстояние грузом за время t. 3. Составляем основное уравнение динамики: 5. Понижаем порядок производной: 4. Проецируем основное уравнение динамики на ось x: или 7 6. Разделяем переменные: 7. Вычисляем интегралы от обоих частей уравнения: 9. Представим проекцию скорости как производную координаты по времени: 10. Вычисляем интегралы от обоих частей уравнения: 9. Разделяем переменные: 8. Определим значение постоянной C1 из начального условия t = 0, vx = v0=0: В итоге получаем уравнение движения (по оси x), которое дает значение пройденного пути за время t: 1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату: 2. Принимаем объект движения за материальную точку (тело движется поступательно), освобождаем от связи (опорной плоскости) и заменяем реакцией (нормальной реакцией гладкой поверхности): 11. Определим значение постоянной C2 из начального условия t = 0, x = x0=0: Пример 3 решения обратной задачи: Сила зависит от координаты. Материальная точка массой m брошена вверх с поверхности Земли со скоростью v0. Сила притяжения Земли обратно пропорциональна квадрату расстояния от точки до центра тяготения (центра Земли). Определить зависимость скорости от расстояния y до центра Земли. 1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату: 2. Составляем основное уравнение динамики: 3. Проецируем основное уравнение динамики на ось y: или Коэффициент пропорциональности можно найти, используя вес точки на поверхности Земли: R Отсюда дифференциальное уравнение имеет вид: или 4. Понижаем порядок производной: 5. Делаем замену переменной: 6. Разделяем переменные: 7. Вычисляем интегралы от обоих частей уравнения: 8. Подставляем пределы: В итоге получаем выражение для скорости в функции от координаты y: Максимальную высоту полета можно найти приравнивая скорость нулю: Максимальная высота полета при обращении знаменателя в нуль: Отсюда при постановке радиуса Земли и ускорения свободного падения получается II космическая скорость:

10 слайд
Лекция 2 (продолжение 2.4) Пример 2 решения обратной задачи: Сила зависит от скорости. Судно массы m имело скорость v0. Сопротивление воды движению судна пропорционально скорости. Определить время, за которое скорость судна упадет вдвое после выключения двигателя, а также пройденное расстояние судном до полной остановки. 8 1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату: 2. Принимаем объект движения за материальную точку (судно движется поступательно), освобождаем от связей (воды) и заменяем реакцией (выталкивающей силой – силой Архимеда), а также силой сопротивления движению. 3. Добавляем активную силу (силу тяжести). 4. Составляем основное уравнение динамики: 5. Проецируем основное уравнение динамики на ось x: или 6. Понижаем порядок производной: 7. Разделяем переменные: 8. Вычисляем интегралы от обоих частей уравнения: 9. Подставляем пределы: Получено выражение, связывающее скорость и время t, откуда можно определить время движения: Время движения, за которое скорость упадет вдвое: Интересно заметить, что при приближении скорости к нулю время движения стремится к бесконечности, т.е. конечная скорость не может быть равна нулю. Чем не “вечное движение”? Однако, при этом пройденный путь до остановки является конечной величиной. Для определения пройденного пути обратимся к выражению, полученному после понижения порядка производной, и сделаем замену переменной: После интегрирования и подстановки пределов получаем: Пройденный путь до остановки: ■ Движение точки, брошенной под углом к горизонту, в однородном поле силы тяжести без учета сопротивления воздуха Исключив время из уравнений движения получаем уравнение траектории: Время полета определяем приравниванием координаты y нулю: Дальность полета определяем подстановкой времени полета:

11 слайд
Лекция 3 Прямолинейные колебания материальной точки – Колебательное движение материальной точки происходит при условии: имеется восстанавливающая сила, стремящая вернуть точку в положение равновесия при любом отклонении ее из этого положения. 9 Восстанавливающая сила есть, положение равновесия устойчивое Восстанавливающей силы нет, положение равновесия неустойчивое Восстанавливающей силы нет, положение равновесия безразличное Восстанавливающая сила есть, положение равновесия устойчивое Необходим анализ Сила упругости пружины – пример линейной восстанавливающей силы. Направлена всегда к положению равновесия, величина прямо пропорциональна линейному удлинению (укорочению) пружины, равному отклонению тела от положения равновесия: с – коэффициент жесткости пружины, численно равный силе, под действием которой пружина изменяет свою длину на единицу, измеряется в Н/м в системе СИ. x y O Виды колебаний материальной точки: 1. Свободные колебания (без учета сопротивления среды). 2. Свободные колебания с учетом сопротивления среды (затухающие колебания). 3. Вынужденные колебания. 4. Вынужденные колебания с учетом сопротивления среды. ■ Свободные колебания – происходят под действием только восстанавливающей силы. Запишем основной закон динамики: Выберем систему координат с центром в положении равновесия (точке O) и спроецируем уравнение на ось x: Приведем полученное уравнение к стандартному (каноническому) виду: Данное уравнение является однородным линейным дифференциальным уравнением II порядка, вид решения которого определяется корнями характеристического уравнения, получаемое с помощью универсальной подстановки: Корни характеристического уравнения мнимые и равные: Общее решение дифференциального уравнения имеет вид: Скорость точки: Начальные условия: Определим постоянные: Итак, уравнение свободных колебаний имеет вид: Уравнение можно представить одночленным выражением: где a – амплитуда, - начальная фаза. Новые константы a и - связаны с постоянными C1 и C2 соотношениями: Определим a и: Причиной возникновения свободных колебаний является начальное смещение x0 и/или начальная скорость v0.

12 слайд
10 Лекция 3 (продолжение 3.2) Затухающие колебания материальной точки – Колебательное движение материальной точки происходит при наличии восстанавливающей силы и силы сопротивления движению. Зависимость силы сопротивления движению от смещения или скорости определяется физической природы среды или связи, препятствующей движению. Наиболее простой зависимостью является линейная зависимость от скорости (вязкое сопротивление): - коэффициент вязкости x y O Основное уравнение динамики: Проекция уравнения динамики на ось: Приведем уравнение к стандартному виду: где Характеристическое уравнение имеет корни: Общее решение данного дифференциального уравнения имеет различный вид в зависимости от значений корней: 1. n < k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n > k – случай большого вязкого сопротивления: - корни действительные, различные. или - эти функции апериодические: 3. n = k: - корни действительные, кратные. эти функции также апериодические:

13 слайд
Лекция 3 (продолжение 3.3) Классификация решений свободных колебаний. Способы соединения пружин. Эквивалентная жесткость. y y 11 Дифф. уравнение Характер. уравнение Корни характ. уравнения Решение дифференциального уравнения График nk n=k

14 слайд
Лекция 4 Вынужденные колебания материальной точки – Наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой. Возмущающая сила может иметь различную природу. Например, в частном случае инерционное воздействие неуравновешенной массы m1 вращающегося ротора вызывает гармонически изменяющиеся проекции силы: Основное уравнение динамики: Проекция уравнения динамики на ось: Приведем уравнение к стандартному виду: 12 Решение этого неоднородного дифференциального уравнения состоит их двух частей x = x1 + x2: x1 – общее решение соответствующего однородного уравнения и x2 – частное решение неоднородного уравнения: Частное решение подбираем в форме правой части: Полученное равенство должно удовлетворяться при любом t . Тогда: или Таким образом, при одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, представляющее собой результат сложения (наложения) свободных (x1) и вынужденных (x2) колебаний. Если p < k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p > k (вынужденные колебания большой частоты), то фаза колебаний противоположна фазе возмущающей силы:

15 слайд
Лекция 4 (продолжение 4.2) 13 Коэффициент динамичности – отношение амплитуды вынужденных колебаний к статическому отклонению точки под действием постоянной силы H = const: Амплитуда вынужденных колебаний: Статическое отклонение можно найти из уравнения равновесия: Здесь: Отсюда: Таким образом, при p < k (малая частота вынужденных колебаний) коэффициент динамичности: При p > k (большая частота вынужденных колебаний) коэффициент динамичности: Резонанс – возникает, когда частота вынужденных колебаний совпадает с частотой собственных колебаний (p = k). Это наиболее часто происходит при запуске и остановке вращения плохо сбалансированных роторов, закрепленных на упругих подвесках. Дифференциальное уравнение колебаний при равенстве частот: Частное решение в форме правой части взять нельзя, т.к. получится линейно зависимое решение (см. общее решение). Общее решение: Подставим в дифференциальное уравнение: Возьмем частное решение в виде и вычислим производные: Таким образом, получено решение: или Вынужденные колебания при резонансе имеют амплитуду неограниченно возрастающую пропорционально времени. Влияние сопротивления движению при вынужденных колебаниях. Дифференциальное уравнение при наличии вязкого сопротивления имеет вид: Общее решение выбирается из таблицы (Лекция 3, стр. 11) в зависимости от соотношения n и к (посмотреть). Частное решение возьмем в виде и вычислим производные: Подставим в дифференциальное уравнение: Приравнивая коэффициенты при одинаковых тригонометрических функциях получаем систему уравнений: Возведением в степень обоих уравнений и сложением их получаем амплитуду вынужденных колебаний: Делением второго уравнения на первое получаем сдвиг фазы вынужденных колебаний: Таким образом, уравнение движения при вынужденных колебаний с учетом сопротивления движению, например при n < k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 слайд
Лекция 5 Относительное движение материальной точки – Положим, что подвижная (неинерциальная) система координат Oxyz движется по некоторому закону относительно неподвижной (инерциальной) системы координат O1x1y1z1. Движение материальной точки M (x, y, z) относительно подвижной системы Oxyz– относительное, относительно неподвижной системы O1x1y1z1– абсолютное. Движение подвижной системы Oxyz относительно неподвижной системы O1x1y1z1– переносное движение. 14 z x1 y1 z1 O1 x y M x y z O Основное уравнение динамики: Абсолютное ускорение точки: Подставим абсолютное ускорение точки в основное уравнение динамики: Перенесем слагаемые с переносным и кориолисовым ускорением в правую часть: Перенесенные слагаемые имеют размерность сил и рассматриваются как соответствующие силы инерции, равные: Тогда относительное движение точки можно рассматривать как абсолютное, если к действующим силам добавить переносную и кориолисову силы инерции: В проекциях на оси подвижной системы координат имеем: Частные случаи относительного движения точки для различного вида переносного движения: 1. Вращение вокруг неподвижной оси: Если вращение равномерное, то εe = 0: 2. Поступательное криволинейное движение: Если движение прямолинейное, то = : Если движение прямолинейное и равномерное, то подвижная система является инерциальной и относительное движение может рассматриваться как абсолютное: Никакими механическими явлениями нельзя обнаружить прямолинейного равномерного движения (принцип относительности классической механики). Влияние вращения Земли на равновесие тел – Положим, что тело находится в равновесии на поверхности Земли на произвольной широте φ (параллели). Земля вращается вокруг своей оси с запада на восток с угловой скоростью: Радиус Земли составляет около 6370 км. S R – полная реакция негладкой поверхности. G – сила притяжения Земли к центру. Ф – центробежная сила инерции. Условие относительного равновесия: Равнодействующая сил притяжения и инерции – сила тяжести (вес): Величина силы тяжести (веса) на поверхности Земли равна P = mg . Центробежная сила инерции составляет малую долю от силы тяжести: Отклонение силы тяжести от направления силы притяжения также мало: Таким образом, влияние вращения Земли на равновесие тел чрезвычайно мало и в практических расчетах не принимается во внимание. Максимальная величина силы инерции (при φ = 0 - на экваторе) составляет всего 0.00343 от величины силы тяжести

17 слайд
Лекция 5 (продолжение 5.2) 15 Влияние вращения Земли на движение тел в поле тяготения Земли – Положим тело падает на Землю с некоторой высоты H над поверхностью Земли на широте φ . Выберем подвижную систему отсчета, жестко связанную с Землей, направляя оси x, y по касательной к параллели и к меридиану: Уравнение относительного движения: Здесь учтена малость центробежной силы инерции по сравнению с силой тяжести. Таким образом сила тяготения отождествляется с силой тяжести. Кроме того, считаем, что сила тяжести направлена перпендикулярно поверхности Земли вследствие малости ее отклонения, как рассмотрено выше. Ускорение Кориолиса равно и направлено параллельно оси y на запад. Сила инерции Кориолиса равна направлена в противоположную сторону. Спроецируем уравнение относительного движения на оси: Решение первого уравнения дает: Начальные условия: Решение третьего уравнения дает: Начальные условия: Третье уравнение принимает вид: Начальные условия: Его решение дает: Полученное решение показывает, что тело при падении отклоняется к востоку. Вычислим величину этого отклонения, например, при падении с высоты 100 м. Время падения найдем из решения второго уравнения: Таким образом, влияние вращения Земли на движение тел чрезвычайно мало для практических высот и скоростей и в технических расчетах не учитывается. Из решения второго уравнения также следует существование скорости по оси y, которая также должна вызывать и вызывает соответствующее ускорение и силу инерции Кориолиса. Влияние этой скорости и силы инерции, связанной с ней, на изменение движения будет еще меньше, чем рассмотренная сила инерции Кориолиса, связанная с вертикальной скоростью.

18 слайд
Лекция 6 Динамика механической системы. Система материальных точек или механическая система – Совокупность материальных точек или материальных тех, объединяемых общими законами взаимодействия (положение или движение каждой из точек или тела зависит от положения и движения всех остальных) Система свободных точек - движение которых не ограничивается никакими связями (например, планетная система, в которой планеты рассматриваются как материальные точки). Система несвободных точек или несвободная механическая система – движение материальных точек или тел ограничиваются наложенными на систему связями (например, механизм, машина и т.п.). 16 Силы, действующие на систему. В дополнение к ранее существовавшей классификации сил (активные и реактивные силы) вводится новая классификация сил: 1. Внешние силы (e) – действующие на точки и тела системы со стороны точек или тел, не входящих в состав данной системы. 2. Внутренние силы (i) – силы взаимодействия между материальными точками или телами, входящими в данную систему. Одна и та же сила может являться как внешней, так и внутренней силой. Все зависит от того, какая механическая система рассматривается. Например: В системе Солнце, Земля и Луна все силы тяготения между ними являются внутренними. При рассмотрении системы Земля и Луна силы тяготения, приложенные со стороны Солнца – внешние: C З Л На основании закона действия и противодействия каждой внутренней силе Fk соответствует другая внутренняя сила Fk’, равная по модулю и противоположная по направлению. Из этого следуют два замечательных свойства внутренних сил: Главный вектор всех внутренних сил системы равен нулю: Главный момент всех внутренних сил системы относительно любого центра равен нулю: Или в проекциях на координатные оси: Замечание. Хотя эти уравнения похожи на уравнения равновесия, они таковыми не являются, поскольку внутренние силы приложены к различным точкам или телам системы и могут вызывать движение этих точек (тел) относительно друг друга. Из этих уравнений следует, что внутренние силы не влияют на движение системы, рассматриваемой как одно целое. Центр масс системы материальных точек. Для описания движения системы в целом вводится геометрическая точка, называемой центром масс, радиус-вектор которой определяется выражением, где M – масса всей системы: Или в проекциях на координатные оси: Формулы для центра масс аналогичны формулам для центра тяжести. Однако, понятие центра масс более общее, поскольку оно не связано с силами тяготения или силами тяжести.

19 слайд
Лекция 6 (продолжение 6.2) 17 Теорема о движении центра масс системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или Просуммируем эти уравнения по всем точкам: В левой части уравнения внесем массы под знак производной и заменим сумму производных на производную суммы: Из определения центра масс: Подставим в полученное уравнение: После вынесения массы системы за знак производной получаем или: Произведение массы системы на ускорение ее центра массе равно главному вектору внешних сил. В проекциях на координатные оси: Центр масс системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему. Следствия из теоремы о движении центра масс системы (законы сохранения): 1. Если в интервале времени главный вектор внешних сил системы равен нулю, Re = 0, то скорость центра масс постоянна, vC = const (центр масс движется равномерно прямолинейно – закон сохранения движения центра масс). 2. Если в интервале времени проекция главного вектора внешних сил системы на ось x равна нулю, Rxe = 0, то скорость центра масс по оси x постоянна, vCx = const (центр масс движется по оси равномерно). Аналогичные утверждения справедливы для осей y и z. Пример: Два человека массами m1 и m2 находятся в лодке массой m3. В начальный момент времени лодка с людьми находилась в покое. Определить перемещение лодки, если человек массой m2 пересел к носу лодки на расстояние а. 3. Если в интервале времени главный вектор внешних сил системы равен нулю, Re = 0, и в начальный момент скорость центра масс равна нулю, vC = 0, то радиус-вектор центра масс остается постоянным, rC = const (центр масс находится в покое – закон сохранения положения центра масс). 4. Если в интервале времени проекция главного вектора внешних сил системы на ось x равна нулю, Rxe = 0, и в начальный момент скорость центра масс по этой оси равна нулю, vCx = 0, то координата центра масс по оси x остается постоянной, xC = const (центр масс не движется по этой оси). Аналогичные утверждения справедливы для осей y и z. 1. Объект движения (лодка с людьми): 2. Отбрасываем связи (воду): 3. Заменяем связь реакцией: 4. Добавляем активные силы: 5. Записываем теорему о центре масс: Проецируем на ось x: O Определим на какое расстояние надо пересесть человеку массы m1, чтобы лодка осталась на месте: Лодка переместится на расстояние l в противоположную сторону.

20 слайд
Лекция 7 Импульс силы – мера механического взаимодействия, характеризующая передачу механического движения со стороны действующих на точку сил за данный промежуток времени: 18 В проекциях на координатные оси: В случае постоянной силы: В проекциях на координатные оси: Импульс равнодействующей – равен геометрической сумме импульсов приложенных к точке сил за один и тот же промежуток времени: Умножим на dt: Проинтегрируем на данном промежутке времени: Количество движения точки – мера механического движения, определяемая вектором, равным произведению массы точки на вектор ее скорости: Теорема об изменении количества движения системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или Количество движения системы материальных точек – геометрическая сумма количеств движения материальных точек: По определению центра масс: Вектор количества движения системы равен произведению массы всей системы на вектор скорости центра масс системы. Тогда: В проекциях на координатные оси: Производная вектора количества движения системы по времени равна главному вектору внешних сил системы. Просуммируем эти уравнения по всем точкам: В левой части уравнения внесем массы под знак производной и заменим сумму производных на производную суммы: Из определения количества движения системы: В проекциях на координатные оси:

21 слайд
Теорема Эйлера – Применение теоремы об изменении количества движения системы к движению сплошной среды (воды) . 1.Выбираем в качестве объекта движения объем воды, находящийся в криволинейном канале турбины: 2. Отбрасываем связи и заменяем их действие реакциями (Rпов – равнодействующая поверхностных сил) 3. Добавляем активные силы (Rоб – равнодействующая объемных сил): 4. Записываем теорему об изменении количества движения системы: Количество движения воды в моменты времени t0 и t1 представим как суммы: Изменение количества движения воды в интервале времени : Изменение количества движения воды за бесконечно малый интервал времени dt: , где F1 F2 Принимая произведение плотности, площади поперечного сечения и скорости за секундную массу получаем: Подставляя дифференциал количества движения системы в теорему об изменении получаем: Следствия из теоремы об изменении количества движения системы (законы сохранения): 1. Если в интервале времени главный вектор внешних сил системы равен нулю, Re = 0, то вектор количества движения постоянен, Q = const – закон сохранения количества движения системы). 2. Если в интервале времени проекция главного вектора внешних сил системы на ось x равна нулю, Rxe = 0, то проекция количества движения системы на ось x постоянна, Qx = const. Аналогичные утверждения справедливы для осей y и z. Лекция 7 (продолжение 7.2) Пример: Граната массы M, летевшая со скоростью v, разорвалась на две части. Скорость одного из осколков массы m1 возросла в направлении движения до величины v1. Определить скорость второго осколка. 1. Объект движения (граната): 2. Объект – свободная система, связи и их реакции отсутствуют. 3. Добавляем активные силы: 4. Записываем теорему об изменении количества движения: Проецируем на ось: β Разделяем переменные и интегрируем: Правый интеграл практически равен нулю, т.к. время взрыва t

22 слайд
Лекция 7 (продолжение 7.3) 20 Момент количества движения точки или кинетический момент движения относительно некоторого центра – мера механического движения, определяемая вектором, равным векторному произведению радиуса-вектора материальной точки на вектор ее количества движения: Кинетический момент системы материальных точек относительно некоторого центра – геометрическая сумма моментов количеств движений всех материальных точек относительно этого же центра: В проекциях на оси: В проекциях на оси: Теорема об изменении момента количества движения системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или Просуммируем эти уравнения по всем точкам: Заменим сумму производных на производную суммы: Выражение в скобках есть момент количества движения системы. Отсюда: Умножим векторно каждое из равенств на радиус-вектор слева: Посмотрим, можно ли вынести знак производной за пределы векторного произведения: Таким образом, получили: Производная вектора момента количества движения системы относительно некоторого центра по времени равна главному моменту внешних сил системы относительно этого же центра. В проекциях на координатные оси: Производная момента количества движения системы относительно некоторой оси по времени равна главному моменту внешних сил системы относительно этой же оси.

23 слайд
Лекция 8 21 ■ Следствия из теоремы об изменении момента количества движения системы (законы сохранения): 1. Если в интервале времени вектор главного момента внешних сил системы относительно некоторого центра равен нулю, MOe = 0, то вектор момента количества движения системы относительно этого же центра постоянен, KO = const – закон сохранения момента количества движения системы). 2. Если в интервале времени главный момент внешних сил системы относительно оси x равен нулю, Mxe = 0, то момент количества движения системы относительно оси x постоянен, Kx = const. Аналогичные утверждения справедливы для осей y и z. 2. Момент инерции твердого тела относительно оси: Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Момент инерции твердого тела относительно оси равен сумме произведений массы каждой точки на квадрат расстояния этой точки до оси. ■ Элементы теории моментов инерции – При вращательном движении твердого тела мерой инерции (сопротивления изменению движения) является момент инерции относительно оси вращения. Рассмотрим основные понятия определения и способы вычисления моментов инерции. 1. Момент инерции материальной точки относительно оси: При переходе от дискретной малой массы к бесконечно малой массе точки предел такой суммы определяется интегралом: осевой момент инерции твердого тела. Кроме осевого момента инерции твердого тела существуют другие виды моментов инерции: центробежный момент инерции твердого тела. полярный момент инерции твердого тела. 3. Теорема о моментах инерции твердого тела относительно параллельных осей – формула перехода к параллельным осям: Момент инерции относительно исходной оси Статические моменты инерции относительно исходных осей Масса тела Расстояние между осями z1 и z2 Таким образом: Если ось z1 проходит через центр масс, то статические моменты равны нулю:

24 слайд
Лекция 8 (продолжение 8.2) 22 Момент инерции однородного стержня постоянного сечения относительно оси: x z L Выделим элементарный объем dV = Adx на расстоянии x: x dx Элементарная масса: Для вычисления момента инерции относительно центральной оси (проходящей через центр тяжести) достаточно изменить расположение оси и задать пределы интегрирования (-L/2, L/2). Здесь продемонстрируем формулу перехода к параллельным осям: zС 5. Момент инерции однородного сплошного цилиндра относительно оси симметрии: H dr r Выделим элементарный объем dV = 2πrdrH (тонкий цилиндр радиуса r) : Элементарная масса: Здесь использована формула объема цилиндра V=πR2H. Для вычисления момента инерции пустотелого (толстого) цилиндра достаточно задать пределы интегрирования от R1 до R2 (R2> R1): 6. Момент инерции тонкого цилиндра относительно оси симметрии (t

25 слайд
Лекция 8 (продолжение 8.3) 23 ■ Дифференциальное уравнение вращения твердого тело относительно оси: Запишем теорему об изменении кинетического момента твердого тела, вращающегося вокруг неподвижной оси: Кинетический момент вращающегося твердого тела равен: Момент внешних сил относительно оси вращения равен вращающему моменту (реакции и сила тяжести моментов не создают): Подставляем кинетический момент и вращающий момент в теорему Пример: Два человека одинакового веса G1 = G2 висят на канате, переброшенном через сплошной блок весом G3 = G1/4. В некоторый момент один из них начал подниматься по канату с относительной скоростью u. Определить скорости подъема каждого из людей. 1. Выбираем объект движения (блок с людьми): 2. Отбрасываем связи (опорное устройство блока): 3. Заменяем связь реакциями (подшипника): 4. Добавляем активные силы (силы тяжести): 5. Записываем теорему об изменении кинетического момента системы относительно оси вращения блока: R Так как момент внешних сил равен нулю, то кинетический момент должен оставаться постоянным: В начальный момент времени t = 0 было равновесие и Kz0 = 0. После начала движения одного человека относительно каната вся система пришла в движение, но кинетический момент системы должен остаться равным нулю: Kz = 0. Кинетический момент системы складывается из кинетических моментов обоих людей и блока: Здесь v2 – скорость второго человека, равная скорости троса, Пример: Определить период малых свободных колебаний однородного стержня массы M и длиной l, подвешенного одним концом к неподвижной оси вращения. Или: В случае малых колебаний sinφ φ: Период колебаний: Момент инерции стержня:

26 слайд
Лекция 8 (продолжение 8.4 – дополнительный материал) 24 ■ Элементарная теория гироскопа: Гироскоп – твердое тело, вращающееся вокруг оси материальной симметрии, одна из точек которой неподвижна. Свободный гироскоп – закреплен так, что его центр масс остается неподвижным, а ось вращения проходит через центр масс и может принимать любое положение в пространстве, т.е. ось вращения изменяет свое положение подобно оси собственного вращения тела при сферическом движении. Основное допущение приближенной (элементарной) теории гироскопа – вектор момента количества движения (кинетический момент) ротора считается направленным вдоль собственной оси вращения. Таким образом, несмотря на то, что в общем случае ротор участвует в трех вращениях, принимается в расчет только угловая скорость собственного вращения ω = dφ/dt. Основанием для этого является то, что в современной технике ротор гироскопа вращается с угловой скоростью порядка 5000-8000 рад/c (около 50000-80000 об/мин), в то время как две другие угловые скорости, связанные с прецессией и нутацией собственной оси вращения в десятки тысяч раз меньше этой скорости. Основное свойство свободного гироскопа – ось ротора сохраняет неизменное направление в пространстве по отношению к инерциальной (звездной) системе отсчета (демонстрируется маятником Фуко, сохраняющим неизменной по отношению к звездам плоскость качания, 1852 г.). Это вытекает из закона сохранения кинетического момента относительно центра масс ротора при условии пренебрежения трением в подшипниках осей подвески ротора, внешней и внутренней рамы: Действие силы на ось свободного гироскопа. В случае действия силы, приложенной к оси ротора, момент внешних сил относительно центра масс не равен нулю: ω ω С Производная кинетического момента по времени равна скорости конца этого вектора (теорема Резаля): Это означает, что ось ротора будет отклоняться не в сторону действия силы, а в сторону вектора момента этой силы, т.е. будет поворачиваться не относительно оси x (внутренняя подвеска), а относительно оси y (внешняя подвеска). При прекращении действия силы ось ротора останется в неизменном положении, соответствующем последнему моменту времени действия силы, т.к. с этого момента времени момент внешних сил вновь становится равным нулю. В случае кратковременного действия силы (удара) ось гироскопа практически не меняет своего положения. Таким образом, быстрое вращение ротора сообщает гироскопу способность противодействовать случайным воздействиям, стремящимся изменить положение оси вращения ротора, а при постоянном действии силы сохраняет положение плоскости, перпендикулярной действующей силе, в которой лежит ось ротора. Эти свойства используются в работе инерциальных систем навигации.
Просмотр: эта статья прочитана 32852 раз
Pdf Выберите язык... Русский Украинский Английский
Полностью материал скачивается выше, предварительно выбрав язык
- Статика
- Основные понятия статики
- Виды сил
- Аксиомы статики
- Связи и их реакции
- Система сходящихся сил
- Методы определения равнодействующей системы сходящихся сил
- Условия равновесия системы сходящихся сил
- Момент силы относительно центра как вектор
- Алгебраическая величина момента силы
- Свойства момента силы относительно центра (точки)
- Теория пар сил
- Сложение двух параллельных сил, направленных в одну сторону
- Сложение двух параллельных сил, направленных в разные стороны
- Пары сил
- Теоремы о паре сил
- Условия равновесия системы пар сил
- Рычаг
- Произвольная плоская система сил
- Случаи приведения плоской системы сил к более простому виду
- Аналитические условия равновесия
- Центр параллельных сил. Центр тяжести
- Центр параллельных сил
- Центр тяжести твердого тела и его координаты
- Центр тяжести объема, плоскости и линии
- Способы определения положения центра тяжести
- Основы рачсетов на прочность
- Задачи и методы сопротивления материалов
- Классификация нагрузок
- Классификация элементов конструкций
- Деформации стержня
- Основные гипотезы и принципы
- Внутренние силы. Метод сечений
- Напряжения
- Растяжение и сжатие
- Механические характеристики материала
- Допускаемые напряжения
- Твердость материалов
- Эпюры продольных сил и напряжений
- Сдвиг
- Геометрические характеристики сечений
- Кручение
- Изгиб
- Дифференциальные зависимости при изгибе
- Прочность при изгибе
- Нормальные напряжения. Расчет на прочность
- Касательные напряжения при изгибе
- Жесткость при изгибе
- Элементы общей теории напряженного состояния
- Теории прочности
- Изгиб с кручением
- Кинематика
- Кинематика точки
- Траектория движения точки
- Способы задания движения точки
- Скорость точки
- Ускорение точки
- Кинематика твердого тела
- Поступательное движение твердого тела
- Вращательное движение твердого тела
- Кинематика зубчатых механизмов
- Плоскопараллельное движение твердого тела
- Сложное движение точки
- Кинематика точки
- Динамика
- Основные законы динамики
- Динамика точки
- Дифференциальные уравнения свободной материальной точки
- Две задачи динамики точки
- Динамика твердого тела
- Классификация сил, действующих на механическую систему
- Дифференциальные уравнения движения механической системы
- Общие теоремы динамики
- Теорема о движении центра масс механической системы
- Теорема об изменении количества движения
- Теорема об изменении момента количества движения
- Теорема об изменении кинетической энергии
- Силы, действующие в машинах
- Силы в зацеплении прямозубой цилиндрической передачи
- Трение в механизмах и машинах
- Трение скольжения
- Трение качения
- Коэффициент полезного действия
- Детали машин
- Механические передачи
- Типы механических передач
- Основные и производные параметры механические передач
- Зубчатые передачи
- Передачи с гибкими звеньями
- Валы
- Назначение и классификация
- Проектный расчет
- Проверочный расчет валов
- Подшипники
- Подшипники скольжения
- Подшипники качения
- Соединение деталей машин
- Виды разъемных и неразъемных соединений
- Шпоночные соединения
- Механические передачи
- Стандартизация норм, взаимозаменяемость
- Допуски и посадки
- Единая система допусков и посадок (ЕСДП)
- Отклонение формы и располож
Формат: pdf
Размер: 4МВ
Язык: русский
Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.
Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.
Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается
Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается
Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы
Определение скорости и ускорения точки по заданным уравнениям движения
Пример решение задачи на определение скорости и ускорения точки по заданным уравнениям движения
Определение скоростей и ускорений точек твердого тела при плоскопараллельном движении
Пример решения задачи на определение скоростей и ускорений точек твердого тела при плоскопараллельном движении
Определение усилий в стержнях плоской фермы
Пример решения задачи на определение усилий в стержнях плоской фермы методом Риттера и методом вырезания узлов
Лекции по теоретической механике
Динамика точки
Лекция 1
Основные понятия динамики
В разделе Динамика изучается движение тел под действием приложенных к ним сил. Поэтому, кроме тех понятий, которые вводились в разделе Кинематика, здесь необходимо использовать новые понятия, отражающие специфику воздействия сил на различные тела и реакцию тел на эти воздействия. Рассмотрим основные из этих понятий.
а) сила
Сила есть количественный результат воздействия на данное тело со стороны других тел. Сила является векторной величиной (рис.1).
![]()
![]()
Точка А начала вектора силы F называется точкой приложения силы . Прямая MN на которой находится вектор силы называется линией действия силы. Длинавектора силы, измеренная в определённом масштабе, называется численным значением или модулем вектора силы . Модуль силы обозначается, как или . Действие силы на тело проявляется либо в его деформации, если тело неподвижно, либо в сообщении ему ускорения при движении тела. На этих проявлениях силы основано устройство различных приборов (силомеров или динамометров) для измерения сил.
б) система сил
Рассматриваемая
совокупность сил образует систему
сил.
Любая система, состоящая из n
сил, может быть записана в следующем
виде:
![]()
в) свободное тело
Тело, которое может перемещаться в пространстве в любом направлении, не испытывая непосредственного (механического) взаимодействия с другими телами, называется свободным или изолированным . Воздействие той или иной системы сил на тело может быть выяснено только в том случае, если это тело свободное .
г) равнодействующая сила
Если какая - либо сила оказывает на свободное тело такое же воздействие, как и некоторая система сил, то эта сила называется равнодействующей данной системы сил . Это записывается следующим образом:
![]() ,
,
что означает эквивалентность воздействия на одно и то же свободное тело равнодействующей и некоторой системы n сил.
Перейдём теперь к рассмотрению более сложных понятий, связанных с количественным определением вращательных воздействий сил.
д) момент силы относительно точки (центра)
Если тело под действием силы может поворачиваться вокруг некоторой неподвижной точки О (рис.2), то для количественной оценки этого вращательного воздействия вводится физическая величина, которая называется моментом силы относительно точки (центра).

Плоскость, проходящая через данную неподвижную точку и линию действия силы, называется плоскостью действия силы . На рис.2 это плоскость ОАВ.
Моментом силы относительно точки (центра) называется векторная величина равная векторному произведению радиус-вектора точки приложения силы на вектор силы:
![]() (1)
(1)
Согласно правилу векторного умножения двух векторов их векторное произведение есть вектор перпендикулярный плоскости расположения векторов сомножителей (в данном случае плоскости треугольника ОАВ), направленный в ту сторону, откуда кратчайший поворот первого вектора сомножителя ко второму вектору сомножителю виден против стрелки часов (рис.2). При таком порядке векторов сомножителей векторного произведения (1), поворот тела под действием силы будет виден против стрелки часов (рис.2)Так как вектор перпендикулярен плоскости действия силы, то его расположение в пространстве определяет положение плоскости действия силы.Численное значение вектора момента силы относительно центра равно удвоенной площади ОАВ и может быть определено по формуле:
![]() ,
(2)
,
(2)
где величина h , равная кратчайшему расстоянию от данной точки О до линии действия силы, называется плечом силы .
Если положение плоскости действия силы в пространстве не существенно для характеристики вращательного воздействия силы, то в этом случае, для характеристики вращательного воздействия силы, вместо вектора момента силы используется алгебраический момент силы :
![]() (3)
(3)
Алгебраический момент силы относительно данного центра равен взятому со знаком плюс или минус произведению модуля силы на её плечо. При этом положительный момент соответствует повороту тела под действием данной силы против стрелки часов, а отрицательный момент повороту тела по стрелке часов. Из формул (1), (2) и (3) следует, что момент силы относительно точки равен нулю только в том случае, когда плечо этой силы h равно нулю . Такая сила не может вращать тело вокруг данной точки.
е) Момент силы относительно оси
Если тело под действием силы может поворачиваться вокруг некоторой неподвижной оси (например, поворот двери или оконной рамы в петлях при их открытии или закрытии), то для количественного определения этого вращательного воздействия вводится физическая величина, которая называется моментом силы относительно данной оси .
 z
z
b F xy
На рис.3 представлена схема, в соответствие с которой определяется момент силы относительно оси z:
Угол образован двумя перпендикулярными направлениями z и к плоскостям треугольников Oab и ОАВ соответственно. Так как Oab является проекцией ОАВ на плоскость xy , то по теореме стереометрии о проекции плоской фигуры на данную плоскость имеем:
где знак плюс соответствует положительному значению cos, т. е. острым углам , а знак минус соответствует отрицательному значению cos, т. е. тупым углам , что обусловлено направлением вектора . В свою очередь SOab =1/2abh , где h ab . Величина отрезка ab равна проекции силы на плоскость xy, т.е. ab = F xy .
На основании вышеизложенного, а так же равенств (4) и (5), определим момент силы относительно оси z следующим образом:
Равенство (6) позволяет сформулировать следующее определение момента силы относительно любой оси: Момент силы относительно данной оси равен проекции на эту ось вектора момента этой силы относительно любой точки данной оси и определяется как взятое со знаком плюс или минус произведение проекции силы на плоскость перпендикулярную данной оси на плечо этой проекции относительно точки пересечения оси с плоскостью проекции. При этом знак момента считается положительным, если, глядя с положительного направления оси, поворот тела вокруг этой оси виден против стрелки часов. В противном случае момент силы относительно оси берётся отрицательным. Поскольку данное определение момента силы относительно оси довольно сложно для запоминания, то рекомендуется запомнить формулу (6) и рис.3, поясняющий эту формулу.
Из формулы (6) следует, что момент силы относительно оси равен нулю, если она параллельна оси (в этом случае её проекция на плоскость перпендикулярную оси равна нулю), или линия действия силы пересекает ось (тогда плечо проекции h =0). Это полностью соответствует физическому смыслу момента силы относительно оси как количественной характеристики вращательного воздействия силы на тело, имеющее ось вращения.
ж) масса тела
Уже давно было замечено, что под действием силы тело набирает скорость постепенно и продолжает движение, если силу убрать. Это свойство тел, сопротивляться изменению своего движения, было названо инерцией или инертностью тел. Количественной мерой инертности тела является его масса. Кроме того, масса тела является количественной мерой воздействия на данное тело гравитационных сил чем больше масса тела, тем большая гравитационная сила действует на тело. Какбудет показано ниже, э ти два определения массы тела связаны между собой.
Остальные понятия и определения динамики будут рассмотрены позднее в тех разделах, где они впервые встретятся.
2. Связи и реакции связей
Ранее в разделе 1 пункт (в) было дано понятие свободного тела, как тела, которое может перемещаться в пространстве в любую сторону, не находясь в непосредственном контакте с другими телами. Большинство реальных тел, окружающих нас, находятся в непосредственном контакте с другими телами и не могут перемещаться в тех или иных направлениях. Так, например, тела, находящиеся на поверхности стола, могут перемещаться в любую сторону, кроме направления, перпендикулярного поверхности стола вниз. Двери, закреплённые на петлях, могут совершать вращательное движение, но не могут двигаться поступательно и т. д. Тела, которые не могут двигаться в пространстве в тех или иных направлениях называются несвободными.
Всё, что ограничивает перемещение данного тела в пространстве, называется связями. Это могут быть какие-либо другие тела, препятствующие перемещению данного тела в некоторых направлениях (физические связи ); в более широком плане, это могут быть некоторые условия, налагаемые на движение тела, ограничивающие это движение. Так, можно поставить условие, чтобы движение материальной точки происходило по заданной кривой. В этом случае связь задаётся математически в виде уравнения (уравнение связи ). Более подробно вопрос о типах связей будет рассмотрен ниже.
Большинство связей, налагаемых на тела, практически, относятся к физическим связям. Поэтому встаёт вопрос о взаимодействии данного тела и связи, наложенной на это тело. На этот вопрос отвечает аксиома о взаимодействии тел: Два тела действуют друг на друга с силами равными по модулю, противоположными по направлению и расположенными на одной прямой. Эти силы называются силами взаимодействия. Силы взаимодействия приложены к разным взаимодействующим телам. Так, например, при взаимодействии данного тела и связи одна из сил взаимодействия приложена со стороны тела к связи, а другая сила взаимодействия приложена со стороны связи к данному телу. Эта последняя сила называется силой реакции связи или, просто, реакцией связи.
При решении практических задач динамики необходимо уметь находить направление реакций различных типов связей. В этом иногда может помочь общее правило определения направления реакции связи: Реакция связи всегда направлена противоположно тому направлению, в котором эта связь препятствует перемещению данного тела. Если это направление можно указать определённо, то и реакция связи будет определена по направлению. В противном случае направление реакции связи неопределённо и может быть найдено только из соответствующих уравнений движения или равновесия тела. Более подробно вопрос о типах связей и направлении их реакций следует изучить по учебнику: С.М. Тарг Краткий курс теоретической механики "Высшая школа", М., 1986г. Гл.1, §3.
В разделе 1 пункт (в) было сказано о том, что полностью определить воздействие какой-либо системы сил можно только в том случае, если эта система сил приложена к свободному телу. Так как большинство тел, реально, являются несвободными, то, чтобы изучить движение этих тел, встаёт вопрос о том, как эти тела сделать свободными. На этот вопрос отвечает аксиома связей лекций по философии на дому. Лекции были... социальной психологии и этнопсихологии. 3. Теоретические итоги В социальном дарвинизме были...
Теоретическая механика
Учебное пособие >> ФизикаКонспект лекций по предмету ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Для студентов специальности: 260501.65 ... - очная Конспект лекций составлен на основе: Буторин Л.В., Бусыгина Е.Б. Теоретическая механика . Учебно-практическое пособие...
